



 Lecture
Lecture
Bio-based aerogels: new eco-friendly porous materials for thermal insulation and controlled release
phone :
fax : 01.60.76.31.50
e-mail : david.ryckelynck@mines-paristech.fr
Centre des Matériaux
MINES Paristech
CNRS UMR 7633
physical address :
63-65 rue Henri Auguste Desbruères
Corbeil-essonnes
mailing address :
BP 87
F-91003 Evry Cedex, France
Mécanique des structures: modélisation hybride à base physique/à base de données, apprentissage automatique pour la réduction de modèle, vision par ordinateur pour la réduction de modèle, réduction adaptative de modèles non linéaires, modèles d'ordre réduit non linéaires pour la propagation d'incertitudes et les simulations multidimensionnelles (surfaces de réponse, aide à la décision,...), hyper réduction, élagage de données issues de la tomographie en mécan, contact, calcul parallèle, modèles d'ordre réduit non linéaires pour le développement durable de la simulation numérique en science des matériaux. Développement de modèles multiphysiques pour la maîtrise des procédés. Modélisation simplifiée des procédés à sollicitation localisée mobile (soudage, frittage laser, cold spray, coupe, ...). Recalage de modèles. Résultats scientifiques récents (novembre 2011). CSDL (janvier 2012).
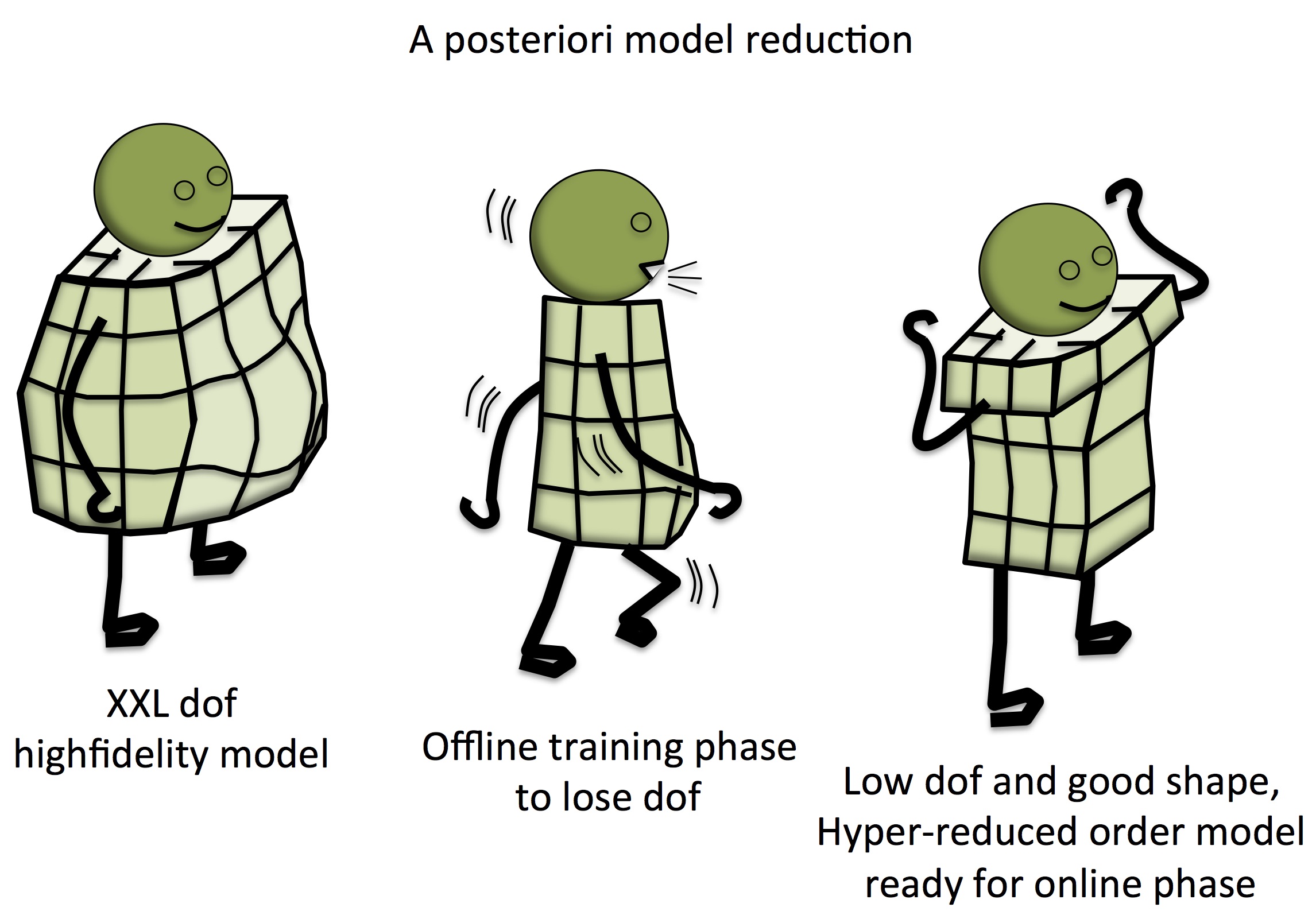
Hyper-reduction in nonlinear mechanics of solid materials. Reduced-order models reveal common features between solutions of parametric partial differential equations (PDE). They aim to save computational time when modelling complex mechanical phenomena, as setting-up convenient nonlinear constitutive equations or boundary conditions for instance.The Garlerkin weak form of nonlinear reduced equations do not provide sufficient speed-up, mainly because the computation of the reduced-residual can’t be performed offline. Hence, this computation remains affected by the complexity of the original model. Hyper-reduction methods aim to generate reduced-order model whose complexity does not depend on the complexity of the original model by introducing a reduced integration domain (RID). This domain contains only few elements of the original mesh.We propose both an explicit hyper-reduced scheme and implicit hyper-reduced schemes applied to nonlinear mechanics of solid materials. The explicit approach aims to interpolate missing boundary conditions on the boundary of the RID. The implicit approach predicts the reduced coordinate of the displacement field by using balance conditions restricted to the RID.
http://mms2.ensmp.fr/option_IDSysCo/accueil_option.php
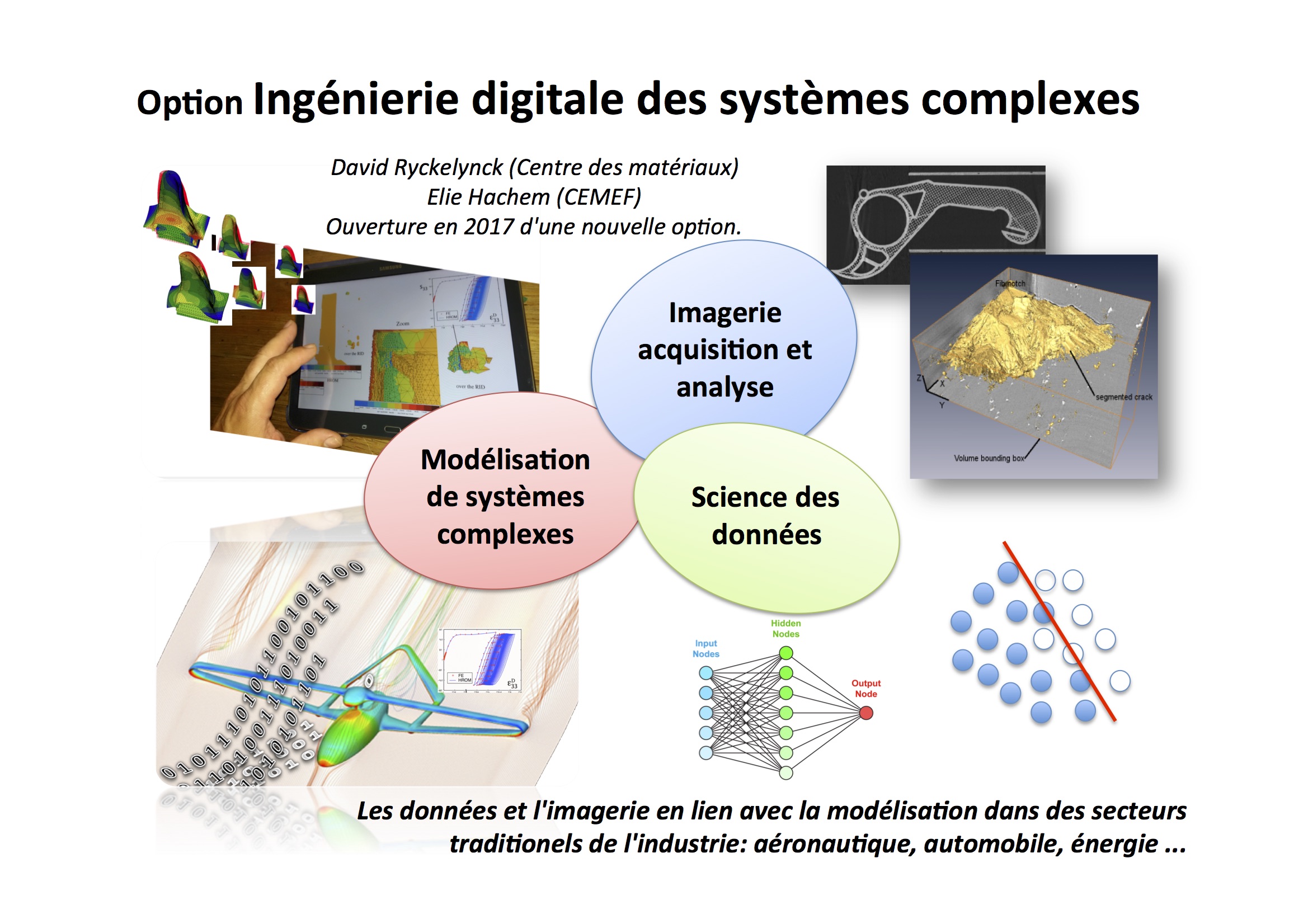
L’option a pour objectif de faire découvrir les algorithmes et les applications en lien avec les transformations digitales de secteurs industriels traditionnels. On s’intéresse à la modélisation numérique de systèmes complexes, dont la conception ou l’exploitation passe par des étapes incontournables de modélisation à fort contenu physique ou multiphysique. Aujourd’hui, les données produites pour ou par ces systèmes sont massives et les technologies pour mieux les valoriser sont facilement disponibles avec des langages informatiques comme le C++ ou le Python. Dans le but d’illustrer avec précision ces transformations, l’option s’appuie en partie sur la mécanique au sens large (fluides, structures, matériaux…). Mais les domaines d’application de cet enseignement sont très vastes. Ainsi, les optionnaires découvrent comment la modélisation de systèmes s’enrichie du rapprochement de la science des données et de l'apprentissage automatique avec le calcul massivement parallèle et l’imagerie. De nouvelles méthodes de travail collaboratif sont en train d’émerger, dans des secteurs où l’exigence de fiabilité des modèles est primordiale (aéronautique, automobile, exploitation de l’énergie nucléaire, transport de polluants potentiels, …).
A new version of the COLD SPRAY CLUB website is now…
The COLD SPRAY CLUB concerns laboratories, technology…
> En savoir +

Formation
A MINES ParisTech PhD student awarded at the…
Josiane Nguejio, PhD student at Centre des Matériaux…
> En savoir +

Recherche
The FEMS Lecturers 2014-2015 include Henry PROUDHON
Lecturer Series This is a scheme which sponsors selected…
> En savoir +
Recherche
award for a team of Centre des Matériaux
Nicolas Gueninchault who work in teams M2 and COCAS with Henry…
> En savoir +
Recherche
The SF2M award three medals to doctors of the centre des…
The medal Réaumur is given by SF2M, each two…
> En savoir +
